Exploring the Shadow Labyrinth

This is an account of one of the more interesting challenges which LRQA encountered during a recent CTF competition run by Hack the Box (the Global Cyber Skills Benchmark CTF 2025: Operation Blackout). It was a reverse engineering exercise, and two artefacts were provided for analysis: 

• An x86-64 ELF file named shadow_labyrinth, and 

• A file of unknown type named file.bin. 

The first part of the flag 

Disassembly of shadow_labyrinth showed that it begins conventionally enough for a CTF challenge: the user is invited to enter a flag, which is then validated for correctness using a hash function and the outcome reported to the user. The task is to invert the hash function and determine what flag needs to be entered for the validation algorithm to report success. 

In this instance there was some trivial validation prior to hashing to check that the entered flag has the correct length and framing. The effect was equivalent to matching against the regular expression /^HTB[{](.{83})[}]$/. The 83 characters of substantive flag content are broken into two parts: the first 48 are hashed immediately, but there was no obvious indication of how the remaining 35 were processed. 

Hashing of the first 48 characters begins with a transposition. They are then divided into groups of 4, and a weighted sum calculated for each group. The weights are random-looking 64-bit integers, and the sums are calculated modulo 264. A list of expected results is provided. For example, the first four characters must satisfy the equation: 

A C++ program was written to solve this by brute force, assuming the four characters to be printable ASCII. No marks are claimed for elegance or efficiency, however since all 48 characters were found in less than a second on modest hardware there was no reason to develop anything more elaborate. 

Decryption and decompression of file.bin 

At this point we had a little over half of the flag. There was no immediately-obvious method for deducing the remainder, however entering the first part correctly does make a difference to the behaviour of the program: instead of failing the validation described above and exiting, it uses the that part of the flag to decrypt the artefact file.bin. 

Decryption is performed using OpenSSL, so the required algorithm (AES256 with CBC) was readily apparent. The only minor complications were: 

• The need to use a specific initialisation vector, and 

• A transposition of the flag which occurs before it is used as the key. 

The resulting plaintext is compressed, but can be decompressed using zlib. 

The virtual machine 

The decrypted and uncompressed content of file.bin is about half a megabyte in size: 

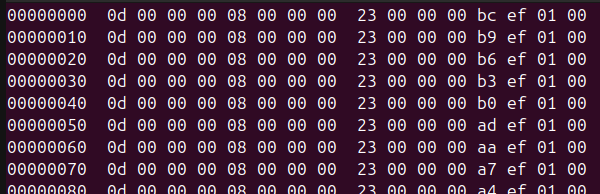
There is some obvious internal structure, but it did not appear to match any well-known file format, and apart from a small quantity of text the meaning was not self-evident. It was therefore necessary to investigate how it was processed by the shadow_labyrinth executable. The key section of code is as follows: 

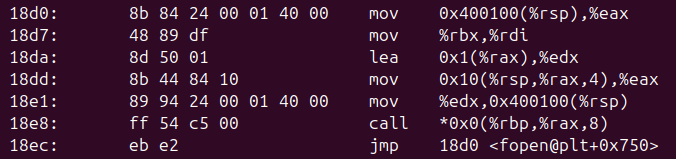
This is an infinite loop which starts at the beginning of the decompressed content, processing it as an array of 32-bit integers. Values from the array are used as indices into a table of function pointers. The table has 16 usable entries: 

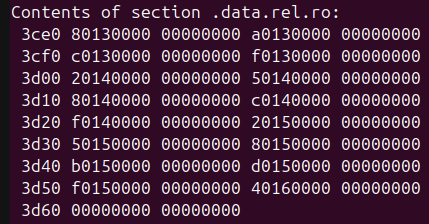
Inspection of these functions showed that many of them consume one or two further 32-bit integers from the array, suggesting the possibility that the loop implements a virtual machine. This was confirmed by detailed reverse engineering of the 16 functions, which revealed the following instruction types: 

• Set value of register to 0 or 1 

• Add, subtract, or logical shift left immediate 

• Add, subtract, or exclusive-OR with register 

• Read from or write to memory 

• Branch if equal, if not equal, or unconditionally 

• Fetch the next character of the flag 

• Write a message to standard output 

• Exit 

Branches and memory accesses are relative to the instruction pointer. Subtraction instructions set a flag to indicate whether the result was zero, and it is this flag which the conditional branch instructions use to determine their behaviour. 

Writing a disassembler 

Although the VM instruction set is Turing-complete, there are strong indications that it is bespoke to this CTF challenge, and therefore the chances of finding any publicly-available tooling for it would be poor. Manual analysis would not have been practicable due to the length of the decompresed file, equating to 47674 instructions. 

Fortunately it is a straightforward matter to write a bespoke disassembler for the instruction set. This is made easier by the fact that there are only 16 instructions, with no variants to be decoded, and although instructions lengths can vary due to the number of arguments, all of the underlying quantities are exactly 32-bits long. An 86-line Python script was sufficient to achieve readable output: 

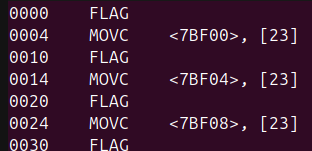
Disassembly: Initial findings 

A full line-by-line analysis of the disassembly would be very time-consuming, but it was possible to deduce some facts about the behaviour of the program through visual inspection: 

• The program begins by reading the second half of the flag into a sequence of 35 memory locations starting at 0x7BF00. 

• There is a single exit instruction, immediately after printing one of the following messages: 

• “[Central Command Node]: Authentication complete!” or 
  ”[Central Command Node]: Authentication failed!” 

• Authentication is successful if and only if the sequence of 35 memory locations starting at 0x7BDE8 compare equal to those starting at 0x7BE74. 

• The code between these was at least somewhat obfuscated, performing sequences of operations which were clearly more complex than necessary such as the following: 

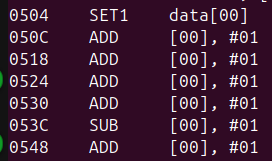
• It could nevertheless be seen that each of the values in the array starting at 0x7BE74 was the sum of 35 other values. 

• At least some of the values feeding into those additions appeared to be the result of multiplications (albeit ones which fail badly if the multiplier is equal to zero): 

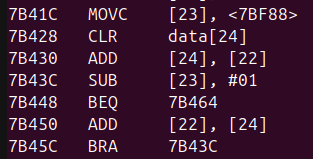
Writing an emulator 

Rather than attempt any automated deobfuscation, the approach taken at this point was to write an emulator for the virtual machine so that practical experiments could be performed to see how its outputs depended on its inputs. This was written in 170 lines of C++, and like the original in the shadow_labyrinth executable it was a simple interpreter, but with the advantage that it could be augmented with code to perform the required experimentation. 

Emulation: Initial findings 

The first and most obvious finding what that the array at 0x7BDE8 did not depend on the flag, and was therefore in effect a set of constants which the array at 0x7BE74 needed to be adjusted to match. For that second array: 

• Every output value depends on every character of the flag. 

• The relationship between any given output and any given input is linear. 

• However, the multipliers are different for every input and every output. 

The multipliers were extracted by running the emulator repeatedly, first with an arbitrary starting value for the flag, and then with one of the characters incremented. The difference between the two outputs gave a vector of 35 multipliers, and repeating this process for each character of the flag gave a matrix of 35 x 35 = 1225 multipliers. 

Further testing showed that there was no constant term added to the result (or rather, that the only constant term was the one already discovered in the array starting at 0x7BDE8). 

Simultaneous equations in 35 unknowns 

The full algorithm can now be described as a matrix multiplication: 

Ax = b 

where A is the matrix of multipliers, x is a vector containing the flag, and b is a vector containing the required result. Equivalently, this can be thought of as a system of 35 simultaneous linear equations in 35 unknowns. 

This is quite similar to the algorithm used for the first half of the flag, but 35 unknowns is too many to be solved using a brute force search. The solution can instead be obtained more efficiently by inverting the multiplier matrix: 

b = A-1 x 

The author’s weapon of choice for this task was NumPy. Rounding was necessary to allow for numerical errors introduced during the matrix inversion. When converted to ASCII this yielded the remainder of the flag, which was accepted by Hack the Box as the correct result.